AI의 두 번의 겨울 - XOR 문제, 기울기 소실 문제

ChatGPT 등장 이후 지금까지 AI는 뜨거운 화두이다. 이전까지는 상상도하지 못했던 것들이 AI를 활용하여 가능해졌고 하루가 멀다하고 새로운 역할을 하는 AI는 출시되고 있다.

AI는 이떻게 이렇게 발전하게 되었을까?

 

인공지능의 탄생

초기의 인공신경망은 단순 on/off 기능의 인공 신경을 그물망 형태로 연결하면 뇌에서 동작하는 간단한 기능을 흉내낼 수 있다는 이론에서 시작되었다.이 신경망 내에서 반복적인 시그널이 발생할 때 신경 세포들은 그 시그널을 기억하는 학습 효과가 있음을 바탕으로 최초의 퍼셉트론이 탄생하게 된다.

 

AI의 첫번째 겨울

허나 퍼셉트론을 통해 AND와 OR 같은 선형 분리가 가능한 문제는 해결할 수 있었지만 XOR 문제에는 적용할 수 없다는 것이 밝혀졌다.

이로 인해 인공지능은 첫번째 겨울을 맞이하게 된다.

 

XOR 문제란?

선형 모델을 활용하여 OR, AND 문제는 해결할 수 있으나 XOR 문제를 해결할 수 없는 문제를 말한다.

 

해결 방안

이후 발견된 XOR 문제의 한계를 극복하는 방법은 바로 좌표 평면 자체에 변화를 주는 것이다. 그러기 위해서는 두 개의 퍼셉트론을 한 번에 계산할 수 있어야 한다. 다층 퍼셉트론을 이용하면 은닉층으로 두개의 퍼셉트론을 한번에 계산할 수 있게 되고 은닉층에서 공간을 외곡해 두 영역을 구분하는 직선을 구할 수 있게 되었다.

 

AI의 두번째 겨울

다중 퍼셉트론과 역전파의 등장으로 XOR 문제가 해결되었으나 신경망이 적용될 수 있는 범위는 한정적이었다. 크고 복잡한 데이터를 다루려면 은닉층을 여러개 연결해야 하는데 이 둘만을 활용해서는 한계가 보이기 시작했다. 또 기울기 소실 문제도 발생하게 되며 AI의 두번째 겨울이 시작된다.

 

기울기 소실 문제란?

역전파 과정에서 출력층에서 멀어질 수록 기울기 값이 매우 작아지는 현상을 말한다. 이는 활성화 함수의 기울기와 관련이 깊은데 그 중 sigmoid함수를 예시로 들어 자세히 알아보자

 

아래는 sigmoid 함수의 그래프와 그의 도함수의 그래프 이다.

sigmoid 함수

sigmoid의 도함수

 

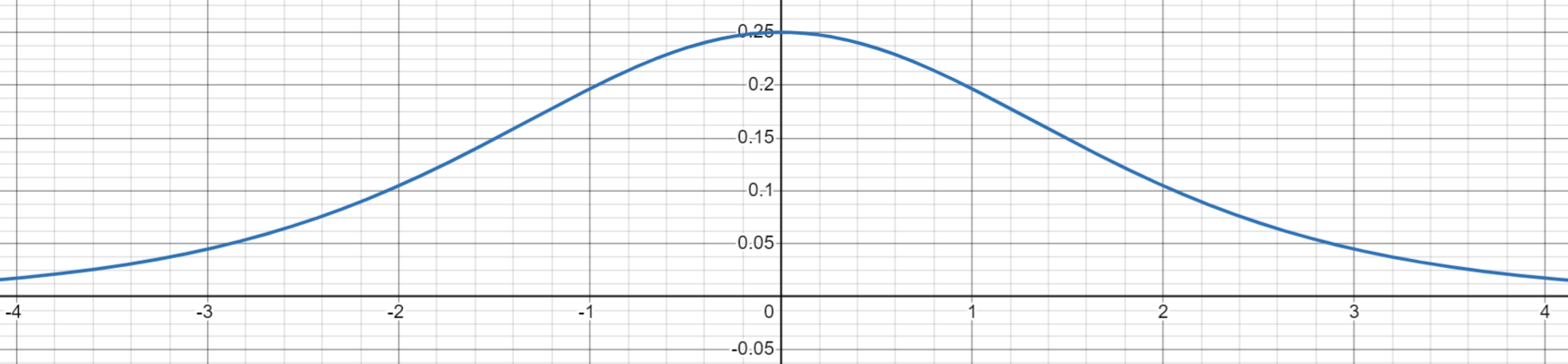
미분 그래프를 확인해보면 sigmoid 함수의 기울기가 최대 0.25이고 최소가 0으로 수렴한다. 역전파에서 입력층에 가까운 앞쪽의 layer로 갈수록 기울기의 값은 거의 0에 가깝게 작아져 가중치 업데이트가 정상적으로 진행되지 않는 것이다.

 

해결방안

이를 해결하기 위해 ReLU 함수가 등장하였다. ReLU 함수와 그의 도함수 그래프는 아래와 같은데

ReLU 함수 그래프

 

ReLU의 도함수 그래프

 

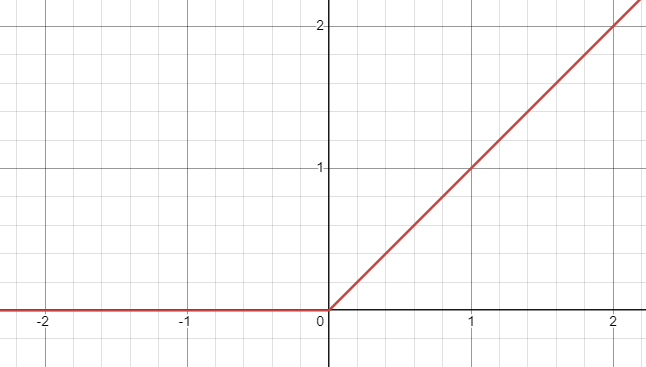
ReLU 함수를 활성화 함수로 사용하면 입력값이 0 이상인 경우 기울기가 0이 되지 않으므로 기울기 소실 문제를 해결할 수 있었다.

 

현대의 딥러닝

이후 2000년대에 이르러 제프리 힌튼의 Deep Belief Network를 기반으로 비지도학습 방법이 가능해진다. 이로 인해 딥러닝이라는 방법론이 인공신경망이라는 명칭을 대체하며 유일하게 여겨지는 방법론으로 칭해진다. 그 이후 Deep-CNN은 이미지 인식 성능 평가에서 2011년에는 26%의 인식 오류율을 4년만에 3.5%로 개선하는 놀라운 성과를 보였다.

 

이런 가능성이 나타나자 구글이 딥마인드 사를 인수하며 시장에 뛰어들었고, 알파고를 개발하여 딥러닝이 많은 사람들에게 알려지게 되었다.

그 후 2017년 구글에서는 트랜스포머를 출시하는데, 트랜스포머는 자연어 처리 분야에서 혁신적인 변화를 가져오게 된다.

이와 관련된 내용은 아래 글에서 자세히 알아보도록 하자. 

[작성 후 링크 추가 예정]

 

 

 

참고 자료

- https://www.samsungsds.com/kr/insights/091517_cx_cvp3.html
- https://www.letr.ai/ko/blog/story-20211029-1
- https://www.letr.ai/ko/blog/story-20211105-1